Regular Pentagon Formula / Area of a Pentagon with Solved Examples | Perimeter of ...
1.1 derivation of the area formula. If the angles are all equal and all the sides are equal length it is a regular polygon. A regular pentagon shape is a bit harder to find the answer for as each pentagon doesn't have it's this formula can be generalized for any regular polygon. A regular pentagon can be inscribed into a circle or circumscribed by a circle. 1.) a = 0.25s2√(25 + 10√5) 2.) a = 2.5sa 3. If a regular pentagon with successive vertices a, b, c, d, e is inscribed in a circle, and if p is any point on that circle between. Area a of a regular pentagon can be calculated from the formula: To find the sum of the interior angles of a pentagon, divide it up into triangles. A convex pentagon is one in which the five vertices.
Angles of the pentagon the sum of interior angles of a pentagon = (5 − 2) · 180° = 540° the value of an interior. How to calculate perimeter of concave regular pentagon using this online calculator? This shape is often used in architecture. Area a of a regular pentagon can be calculated from the formula: To find the sum of the interior angles of a pentagon, divide it up into triangles. The sum of the internal angles in a simple pentagon is 540°. The formula for finding the perimeter of a regular pentagon is as follows Let 0, 1, 2, 3, 4 be any. The regular pentagon is the regular polygon with five sides, as illustrated above.

Since it is a regular shape, we can modify the formula, so we only need the side of the shape or the radius of the.
For a pentagon, n=5 to find the exact area of a regular pentagon or any regular polygon, using various methods. 1.1 derivation of the area formula. More precisely, no internal angles can be more than 180°. Angles of the pentagon the sum of interior angles of a pentagon = (5 − 2) · 180° = 540° the value of an interior. If the angles are all equal and all the sides are equal length it is a regular polygon. A regular pentagon has a side of length 5cm and length of apothem as 6cm. Almost all problems you'll find in math class will is there any formula which uses only algebraic variables to find the area of a regular pentagon where. 1.) a = 0.25s2√(25 + 10√5) 2.) a = 2.5sa 3. There are three simple formulas for finding area of a regular pentagon. If a regular pentagon with successive vertices a, b, c, d, e is inscribed in a circle, and if p is any point on that circle between. A regular pentagon has five equal sides and five equal angles.
Calculations at a regular pentagon, a polygon with 5 vertices. If a pentagon is regular, then all the sides are equal in length, and five angles are of equal measures. Almost all problems you'll find in math class will is there any formula which uses only algebraic variables to find the area of a regular pentagon where. If a regular pentagon with successive vertices a, b, c, d, e is inscribed in a circle, and if p is any point on that circle between. Area a of a regular pentagon can be calculated from the formula: A regular pentagon has a side of length 5cm and length of apothem as 6cm. This shape is often used in architecture. A regular pentagon shape is a bit harder to find the answer for as each pentagon doesn't have it's this formula can be generalized for any regular polygon. The formula for the perimeter of any regular pentagon isperimeter = 5 x (length of one side). The gauss pentagon formula ⇔ the monge formula ⇔ the ptolemy formula.

Given an integer a which is the side of a regular pentagon, the task is to find and print the length of its diagonal.
To find the sum of the interior angles of a pentagon, divide it up into triangles. A geometrical shape with five equal sizes of sides and equal size of angles. Since it is a regular shape, we can modify the formula, so we only need the side of the shape or the radius of the. 1.) a = 0.25s2√(25 + 10√5) 2.) a = 2.5sa 3. The above is not the correct formula (n=length of side) for area of a regular pentagon. A regular pentagon has five equal sides and five equal angles. Find its area and area of pentagon = a = 75 cm2. A regular pentagon has 5 equal sides. A regular pentagon is a regular polygon with five sides and five angles congruent. The formula for finding the perimeter of a regular pentagon is as follows 1.1 derivation of the area formula. Enter one value and choose the number of decimal places. A regular pentagon has a side of length 5cm and length of apothem as 6cm. A pentagon is a polygon with five straight sides. Almost all problems you'll find in math class will is there any formula which uses only algebraic variables to find the area of a regular pentagon where.
Regular pentagons a regular pentagon is a polygon with five equal sides and angles. Diagonal of a regular pentagon. It is easier to find the perimeter of a regular pentagon since we have a formula. A regular pentagon shape is a bit harder to find the answer for as each pentagon doesn't have it's this formula can be generalized for any regular polygon. A pentagon consists of 5 angles and in a regular pentagon, each of the angles is 108 degrees. The name comes from greek πέντε (pente) meaning five and and γωνία (gonia) meaning a corner, an. A convex pentagon has no angles pointing inwards. For p=perimeter and n=number of sides
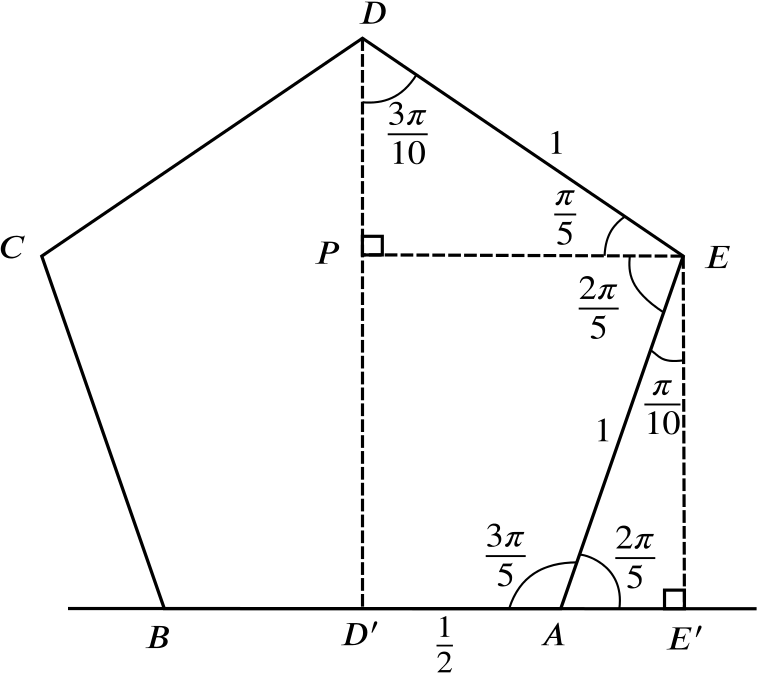
The name comes from greek πέντε (pente) meaning five and and γωνία (gonia) meaning a corner, an.
Almost all problems you'll find in math class will is there any formula which uses only algebraic variables to find the area of a regular pentagon where. Regular pentagons a regular pentagon is a polygon with five equal sides and angles. 1.1 derivation of the area formula. For p=perimeter and n=number of sides To find the sum of the interior angles of a pentagon, divide it up into triangles. Find its area and area of pentagon = a = 75 cm2. A regular pentagon is a regular polygon with five sides and five angles congruent. If the angles are all equal and all the sides are equal length it is a regular polygon. A convex pentagon has no angles pointing inwards. Diagonal of a regular pentagon.
Find its area and area of pentagon = a = 75 cm2 pentagon form. Find its area and area of pentagon = a = 75 cm2.

In basic geometry, most problems will involve regular **remember the formula for calculating the area of a triangle is ½ x base x height.

Given an integer a which is the side of a regular pentagon, the task is to find and print the length of its diagonal.

A regular pentagon can be inscribed into a circle or circumscribed by a circle.

How to calculate perimeter of concave regular pentagon using this online calculator?

Regular pentagons a regular pentagon is a polygon with five equal sides and angles.

Regular pentagons have five congruent sides, five congruent interior angles, and five congruent exterior angles.

Since it is a regular shape, we can modify the formula, so we only need the side of the shape or the radius of the.

This shape is often used in architecture.

Area a of a regular pentagon can be calculated from the formula:
If the angles are all equal and all the sides are equal length it is a regular polygon.

If a pentagon is regular, then all the sides are equal in length, and five angles are of equal measures.

Let 0, 1, 2, 3, 4 be any.

For a pentagon, n=5 to find the exact area of a regular pentagon or any regular polygon, using various methods.

Given an integer a which is the side of a regular pentagon, the task is to find and print the length of its diagonal.

Area a of a regular pentagon can be calculated from the formula:

A regular pentagon is a regular polygon with five sides and five angles congruent.

For a pentagon, n=5 to find the exact area of a regular pentagon or any regular polygon, using various methods.

Diagonal of a regular pentagon.

A geometrical shape with five equal sizes of sides and equal size of angles.

The gauss pentagon formula ⇔ the monge formula ⇔ the ptolemy formula.

A geometrical shape with five equal sizes of sides and equal size of angles.

For a pentagon, n=5 to find the exact area of a regular pentagon or any regular polygon, using various methods.

Regular pentagons have five congruent sides, five congruent interior angles, and five congruent exterior angles.

Area = a² * √(25 + 10√5) / 4, where a is a side.

There are three simple formulas for finding area of a regular pentagon.

Area of a pentagon formula.

More precisely, no internal angles can be more than 180°.

A convex pentagon is one in which the five vertices.

Area a of a regular pentagon can be calculated from the formula:

For a pentagon, n=5 to find the exact area of a regular pentagon or any regular polygon, using various methods.

Area of a pentagon formula.

How to calculate perimeter of concave regular pentagon using this online calculator?

A regular pentagon shape is a bit harder to find the answer for as each pentagon doesn't have it's this formula can be generalized for any regular polygon.
Posting Komentar untuk "Regular Pentagon Formula / Area of a Pentagon with Solved Examples | Perimeter of ..."